Quantum Computer Algorithms: Part 1 - Quasi-Classical Methods

by Dave D'Rave

The operations which can be performed by a quantum computer are a superset of those which can be performed by a classical computer.

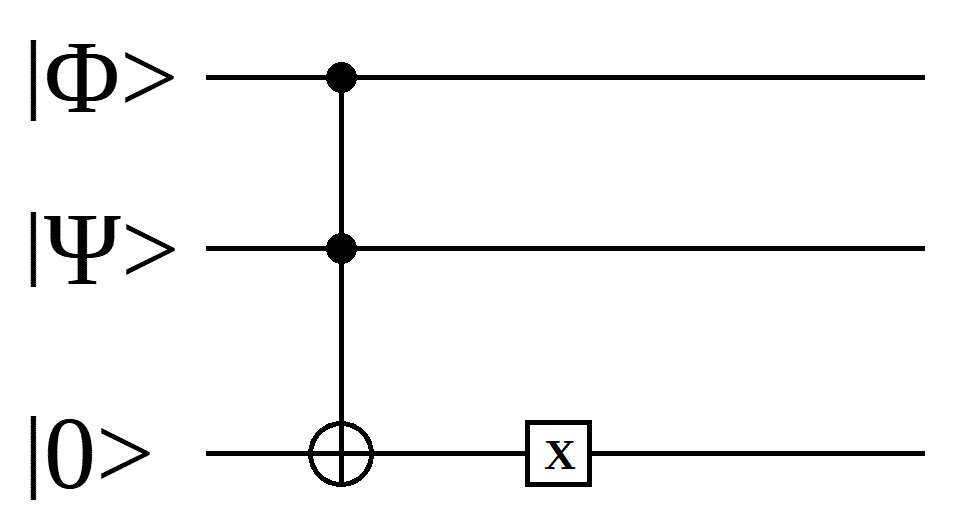
This means that any operation which can be performed by classical boolean gates can be performed by quantum gates.  For example, a standard 7400 NAND gate can be implemented as a series of quantum gates:

(This is a Toffoli gate, followed by a NOT gate.  Wikipedia has a pretty good article on the subject of quantum gates in general, and Toffoli gates in particular.)

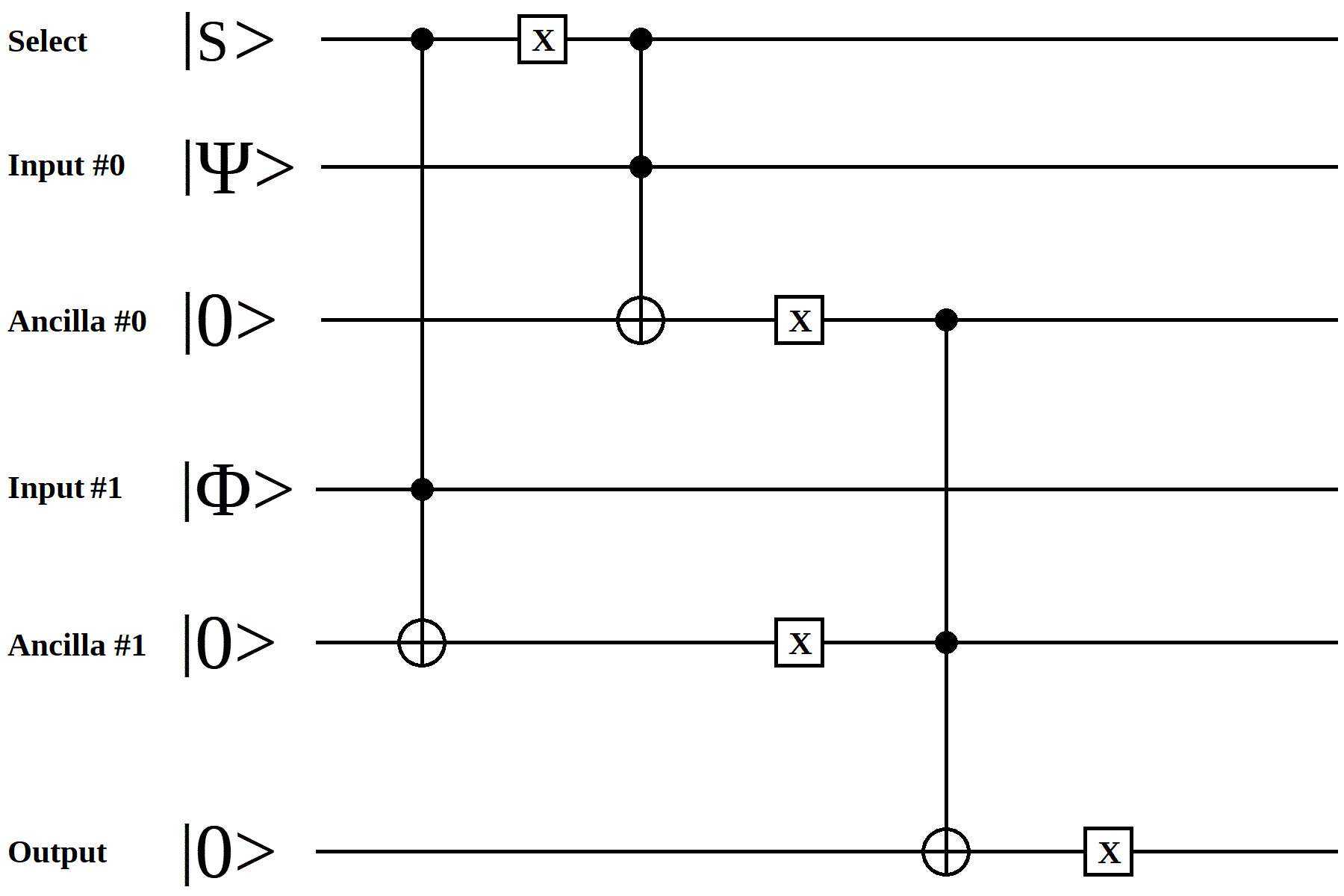
To give another example, you can implement select logic, similar to the 74157, as:

The operation of this circuit is that, if the Select is |0⟩ (in Dirac Notation), then the output will be Input #0, and if the Select is |1⟩, then the output will be Input #1.

If you look closely, you can see that this is a logical AND-OR-SELECT, or a 3-NAND-SELECT.

The point of this is to show that any circuit build out of classical logic can be translated into an equivalent quantum logic circuit.

Superposition and Logic Superposition

Compared with classical logic, various additional capabilities exist when using quantum logic.

One major difference between classical and quantum logic is superposition.

If the select input from the example above has a value of k * (|0⟩ + |1⟩), then the output will be an equal combination of the two inputs.

If the select input is k * (9.0 * |0⟩ + |1⟩), then the output will be a combination of mostly Input #0 and a small amount of Input #1.

Another difference comes from the fact that quantum logic operates on data items which contain both amplitude and phase information.  This is usually expressed by the use of imaginary numbers.  In particular, a full set of quantum logic will contain "phase rotation" operators and may contain "phase reflection" operators.  Because imaginary numbers support the square root of negative numbers, the quantum logic set contains functions like "the square root of NOT."

Entanglement

Another difference between classical and quantum logic is called entanglement.

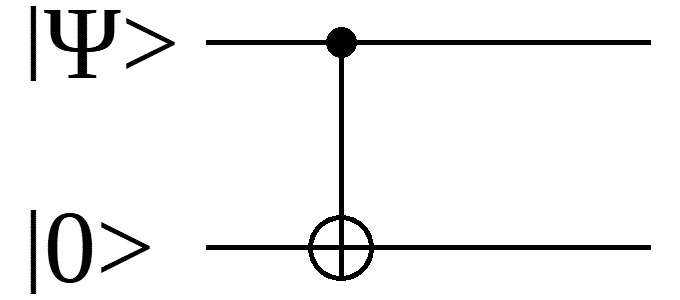
Two qubits are said to be entangled if the act of measuring one of them gives you information about the other one.  A very simple example is the case of a CNOT gate:

In this example, the outputs will be the same as the input.

That seems to be the same as a classical buffer, but there is an important difference: If you measure one of the qubits, then you have obtained information about the other qubit.  This information has a statistical character, and is present even if one of the qubits has been processed before being measured.

The practical effect of entanglement is that multi-qubit data objects can be treated as being a single unit.  For example, it you have a 32-qubit quantum register, it is generally not possible to measure one of the qubits without affecting the others.  (This is often a nuisance, because you cannot clone a quantum state.  It can also be useful for operations like quantum teleportation or quantum steering.)

In situations in which we are processing n-qubit integers or bit strings, the internal entanglement of the qubits can be used to perform partial or conditional measurements.

Consider a 32-qubit register which contains a 50 percent density of |0⟩ and a 50 percent density of |some random number⟩.

If you measure one of the qubits and it turns out to be zero, you have constrained the system, but the remaining qubits continue to be in a superposition state.

On the other hand, if your measurement turns out to be one, then you can be sure that the remaining bits encode |some random number⟩, and not |0⟩.

This sort of thing is described as "partial measurement," or "partial waveform collapse," and features in many Einstein-Podolsky-Rosen (EPR) experiments.

Superposition of Entangled Data

Useful quantum computer systems require the ability to create, manipulate, and measure multi-qubit data which contains a superposition of entangled data items.

For example, consider a 32-qubit register which is interpreted as an integer.  We want to load it with the set of all prime numbers which fit into 32 bits.

This would be |2, 3, 5, 7, 11, 13 ... ⟩, or |all primes between 2 and 4G⟩.

Then consider what happens if you take |all the primes⟩ and add 21 to it.  At that point, there is no easy way to describe the bit relations or their entanglement.  If you take |all the primes⟩ and multiply by five, it is even harder.

Practical quantum computer algorithms need to be able to deal with these types of data items.

Oracle Methods

A fairly common type of quantum algorithm is called the oracle.

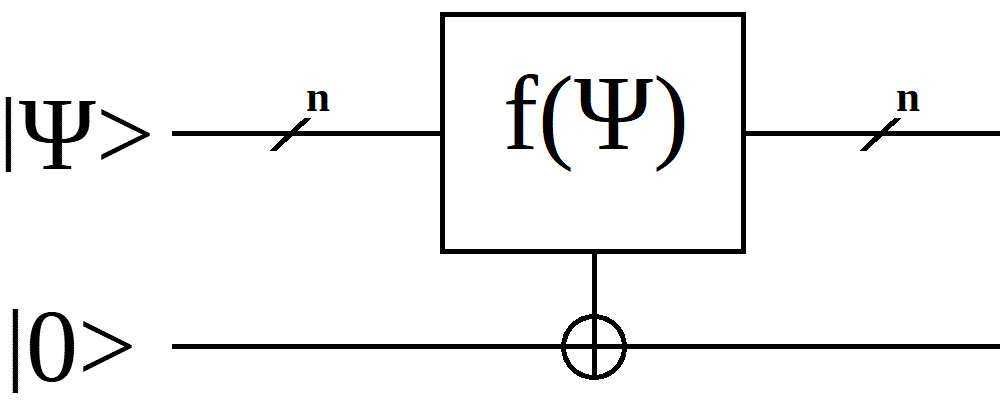
This is defined as a function which has a large number of inputs and only one output.

An oracle is generically implemented as:

Note that the input set can be a group of qubits (complex numbers), classical bits (real numbers), or a mixture of the two.

Note that the output may be |0⟩, |1⟩, or a superposition of the two.

Note that the output may be an imaginary number or a complex number.

Oracles are frequently used for set theory operators, such as "Does the input group contain an integer which is less than 127?" or "Does the input group, considered as eight-bit fields, contain only printable ASCII data?" or even "Is the input group a word in the English language?"

Conclusion

Quantum algorithms are able to do anything which can be done using classical algorithms, and can also perform operations involving complex numbers, superposition, and entanglement.

One common approach for including an existing classical algorithm into a quantum system is to wrap the classical function inside of a quantum oracle.

Quantum Computer Algorithms: Part 2 - Amplitude Amplification